در مقاله قبلی درباره ریز حالت ها صحبت کردیم و مقدماتی را در رابطه با جملات طیفی و اهمیت آنها در شیمی معدنی عنوان کردیم. در این مقاله قصد داریم تا در رابطه با جفت شدن اسپین اوربیت یا همان جفت شدگی راسل ساندرز صحبت کنیم.
جفت شدگی راسل ساندرز چیست؟
می دانیم که در یک اتم معین، تعدادی الکترون وجود دارد. این الکترون ها به طور مستقل، هر کدام دارای اسپین مشخص مثبت و یا منفی هستند. اگر بخواهیم به اسپین تک به تک آن ها توجه کنیم و آن ها را در محاسبات مان لحاظ کنیم؛ کاری دشوار و بی فایده خواهیم داشت.
چرا که همه این اسپین ها به صورت تک به تک، رفتار اتم را مشخص نکرده بلکه به صورت یک اثر جمعی مشاهده می شود. بنابراین بهترین کار این است که همه این اسپین ها را در قالب یک اسپین جمعی برای اتم در آورده و از آن استفاده کنیم.
بنابراین همه اسپین ها را با هم جمع کرده و در قالب یک اسپین کلی تعریف می کنیم و آن را با نماد S مشخص می کنیم. و برای آن داریم:
همچنین می دانیم که هر یک از این الکترون ها در یک اوربیتال وجود قرار گرفته و این اوربیتال، یک عدد کوانتومی اوربیتالی معین دارد. از آنجایی که کار کردن با تک تک الکترون ها کاری بسیار سخت و بیهوده است و بنابراین ما عدد کوانتومی اوربیتالی همه الکترون ها را جمع کرده و به صورت یک عدد کوانتومی اوربیتالی خاص عنوان کرده و آن را به همه اتم نسبت می دهیم.
تا به اینجا یک اسپین جمعی و یک عدد کوانتومی اوربیتالی جمعی داریم.
ما می دانیم که الکترون در اطراف هسته، با دو حالت مختلف چرخش میکند. یکی چرخش به دور خودش است که در قالب اسپین ظاهر می شود و دیگری چرخش به دور هسته اتم است که در قالب عدد کوانتومی اوربیتالی ظاهر می شود.
ما برای هر یک از این ها یک عدد به دست آورده ایم که حاصل اثر جمعی اسپین ها و اثر جمعی عدد های کوانتومی اوربیتالی است. این دو عدد، کاربرد بسیار زیادی دارند؛ اما ما می توانیم به نحو دیگری نیز به حرکت الکترون ها نگاه کنیم.
جفت شدن اسپین اسپین
برای یک سیستم چند الکترونی، اندازه حرکت اسپینی کل، از جفت شدن اندازه حرکت اسپینی تک به تک الکترون ها به دست می آید و داریم:
برای مثال، اگر یک سیستم دو الکترونی مثل اتم هلیوم را در نظر بگیریم. دو الکترون داریم که اسپین آن ها می تواند مثبت و یا منفی باشد؛ بنابراین دو حالت ممکن است. اول این که اسپین هر دو آن ها موازی باشد که در این صورت، عدد اندازه حرکت اسپین کل، برابر با 1 است. در حالت دیگر، اسپین این دو الکترون مخالف یکدیگر است که در این صورت، عدد اندازه حرکت اسپین کل برابر با 0خواهد بود.
در بحث جملات طیفی، ما به عدد اندازه حرکت اسپینی کل کاری نداریم بلکه با عدد دیگری تحت عنوان چندگانگی اسپین سر و کار داریم که با فرمول زیر مشخص میشود و برای ما اهمیت زیادی دارد. توجه کنید که S در فرمول زیر S بزرگ است. یعنی حاصل جمع اسپین ها را باید در فرمول زیر استفاده کنیم.
جفت شدن اوربیت اوربیت
همانطور که در بالا عنوان کردیم؛ ما اثر تک به تک اعداد کوانتومی اوربیتالی را در نظر نمی گیریم. بلکه اثر جمعی اعداد کوانتومی اوربیتالی را در یک عدد واحد، به صورت عدد کوانتومی اوربیتالی کل در نظر می گیریم و برای محاسبه آن داریم:
ما با استفاده از این فرمول، برای اعداد کوانتومی اوربیتالی مختلف، نتایج مختلفی را به دست می آوریم. به عنوان مثال، اگر برای یک سیستم دو الکترونی با آرایش p2 دست به کار شویم؛ مقادیر 0 و 1 و 2 را به دست می آوریم. اما چگونه؟
ما می دانیم که الکترون در اوربیتال های p می تواند اعداد کوانتومی اوربیتالی 1 و 0 و یا 1- داشته باشد. بنابراین اگر به جای l های فرمول بالا اعداد 1 و 0 و یا 1- را ذکر کنیم؛ در نهایت مقادیر 0 و 1 و 2 را به دست می آوریم.
مهم است بدانید که برای عدد اندازه حرکت کوانتومی اوربیتالی کل، ما دیگر از از اعداد ریاضی استفاده نمی کنیم؛ بلکه آن را به صورت یک حرف انگلیسی نمایش می دهیم. شما مشابه این کار را قبلاً در در مورد اعداد کوانتومی اوربیتالی انجام داده اید.
در آن جا برای عدد کوانتومی اوربیتالی 0 حرف s برای عدد 1 حرف p و… را پذیرفتید. حالا در این جا نیز مشابه آن را داریم؛ برای عدد 1 حرف S برای عدد 1 حرف P برای عدد 2 حرف D و همینطور برای اعداد بالاتر، حروف بعدی زبان انگلیسی را بیان می کنیم (به صورت حروف بزرگ).
مثال بالا برای یک سیستم دو الکترونی با آرایش p2، ما اعداد 0 و 1 و 2 را به دست آورده ایم. بنابراین آن ها را با حروف S و P و D معرفی می کنیم.
جفت شدگی اسپین اوربیت ( جفت شدگی راسل ساندرز)
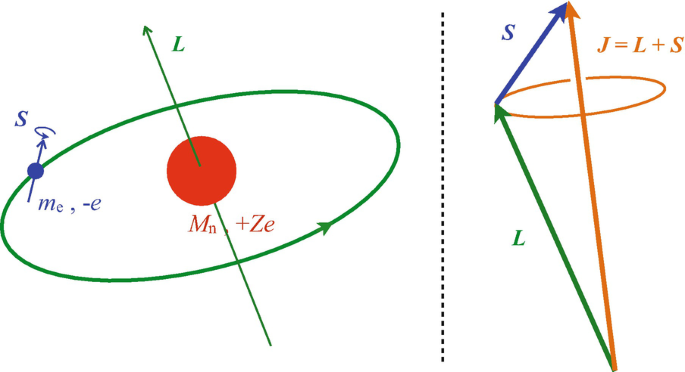
در این نوع جفت شدگی، عدد کوانتومی اوربیتالی کل (L) با عدد اسپین کل (S) جمع شده و در قالب یک عدد مشخص آورده می شود که به آن، اندازه حرکت زاویه ای کل (j) گفته می شود. در این حالت، چنین تصور میشود که انگار ما گردش الکترون به دور خود و به دور هسته اتم را ترکیب کرده ایم؛ برای درک بهتر به تصویر زیر توجه کنید.
این عمل باعث می شود تا کارهای محاسباتی بسیار جالب و ساده ای انجام دهیم که منجر به نتایج منحصر به فردی می شود. در ادامه به تفضیل در رابطه با هر یک از آن ها صحبت می کنیم. برای محاسبه این عدد داریم:
در بحث جملات طیفی، توجه داشته باشید که ما قرار نیست فقط به حالت های ممکن و یا مجاز بپردازیم. بلکه ما همه حالت ها را در نظر گرفته و سپس از میان آن ها، جملات طیفی ممکن و جملات طیفی غیرممکن را اعلام کرده و بر اساس قواعد مشخصی معرفی می کنیم.
در نهایت برای هر معرفی جملات طیفی از یک فرمول کلی و واحد به صورت زیر استفاده می کنیم که در مقالات بعدی بیشتر درباره آن صحبت خواهیم کرد.
تعداد کل ریز حالت ها
حال با داشتن اعداد S و L می توانیم یک فرمول واحد داشته باشیم که با آن تمام ریز حالت های یک فرم خاص را به دست بیاوریم. آن فرمول به صورت زیر است:
البته با فرمول دیگری که مبتنی بر j است نیز می توان تما ریز حالت ها را حساب کرد. در این صورت داریم:
در مقالات بعدی درباره این که حروف و اعداد گفته شده در اینجا و این که چه کاربردی دارند صحبت خواهیم کرد.
به این پست چند تا ستاره میدی؟
برای امتیاز دهی روی ستاره ها کلیک کن
امتیاز میانگین 5 / 5. تعداد رای ها 2


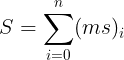





1 دیدگاه در “بررسی کامل جملات طیفی در شیمی معدنی (قسمت دوم: جفت شدگی راسل ساندرز)”
عالی بود