ADD ANYTHING HERE OR JUST REMOVE IT…

ورود / ثبت نام

0 محصول 0 ریال

0 محصول 0 ریال

تماس با پشتیبانی

سینتیک واکنش های مرتبه اول

واکنش مرتبه اول چگونه واکنشی است؟

فرض کنید یک واکنش مرتبه اول به صورت زیر داشته باشیم که در آن a و b ضرایب استوکیومتری مواد A و B و k ثابت سرعت انجام واکنش باشد.

$\large aA\overset{k}{\rightarrow} bB$

در این صورت برای بیان سرعت انجام واکنش، از نسبت تغییرات غلظت یکی از گونه ها، نسبت به زمان استفاده می کنیم و داریم: $\large R=-\frac{1}{a}\frac{d[A]}{dt}$

علامت منفی بخاطر این است که در طی واکنش غلظت گونه A کاهش می یابد. به طور مشابه برای گونه B داریم:

$\large R=\frac{1}{b}\frac{d[B]}{dt}$

در اینجا عدم وجود علامت منفی بخاطر این است که در گذر زمان، گونه B تولید می شود. همچنین برای بیان سرعت این واکنش می توان از رابطه قانون سرعت به صورت زیر استفاده کرد و داریم:

$\large R=k[A]$

از قرار دادن تساوی بین دو معادله مربوط به R داریم:

$\large R=k[A]=-\frac{1}{a}\frac{d[A]}{dt}$

در این صورت به ازای ضریب استوکیومتری 1 برای گونه A داریم:

$\large k[A]=-\frac{d[A]}{dt} {\color{Red} \rightarrow} \frac{d[A]}{[A]}=-kdt$

می توان از قسمت آخر معادله انتگرال گرفت؛ در این صورت داریم:

$\large \int_{[A]_{0}}^{[A]}\frac{d[A]}{[A]}=-k\int_{0}^{t}dt$

با حل انتگرال در نهایت داریم:

$\large -kt=Ln (\frac{[A]}{[A]_{0}})$

اگر از دو طرف معادله e بگیریم در نهایت داریم:

$\large e^{-kt}=\frac{[A]}{[A]_{0}}{\color{Red} \rightarrow } {\color{Blue} [A]={[A]_{0}} e^{-kt}}$

با رابطه (قسمت آبی رنگ) بالا می توان غلظت گونه A را در هر لحظه محاسبه کرد.

زمان نیمه عمر: مدت زمانی که طول می کشد تا غلظت گونه واکنش دهنده به نصف مقدار اولیه اش برسد.

در یک واکنش مرتبه اول برای زمان نیمه عمر داریم:

$\large t_{1/2}=\frac{0.693}{k}$

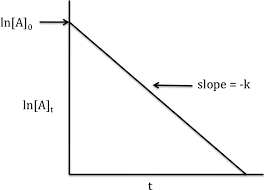
اگر غلظت گونه B بر حسب زمان را برای یک واکنش مرتبه اول رسم کنیم داریم:

در این نمودار، شیب خط برابر با k است. توجه کنید که اگر همین نمودار را برای گونه A رسم کنیم. از صفر شروع می شود و با همین شیب به بالا می رود.

به این پست چند تا ستاره میدی؟

برای امتیاز دهی روی ستاره ها کلیک کن

امتیاز میانگین 1 / 5. تعداد رای ها 1

دیدگاهتان را بنویسید لغو پاسخ

برخی محصولات فروشگاه

افزودن به سبد خرید

مشاهده سریع

تفسیر طیف XRD

2,500,000 ریال

افزودن به سبد خرید

مشاهده سریع

تفسیر آنالیز GC

2,500,000 ریال

افزودن به سبد خرید

مشاهده سریع

تفسیر آنالیز XRF

2,500,000 ریال

افزودن به سبد خرید

مشاهده سریع

تفسیر تست BET

2,500,000 ریال